Quadratic Programming Solver for Non-negative Matrix Factorization with Spark
Debasish Das Santanu Das
debasish.das@verizon.com santanu.das@verizon.com
Big Data Analytics
Verizon
Roadmap
- Some overview on Matrix Factorization
- QP formulation of Non-negative Matrix Factorization (NMF)
- Algorithms to solve quadratic programming problems
Roadmap
- Some overview on Matrix Factorization
- QP formulation of Non-negative Matrix Factorization (NMF)
-
Algorithms to solve quadratic programming problems
- Some QP Applications (on MovieLens data)
- unconstrained
- linear constrained
- Results & Discussions
Matrix Factorization
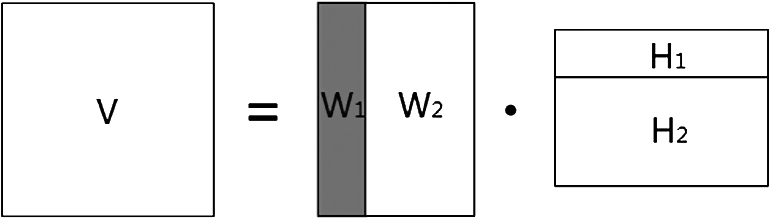
What is it- To decompose observed data (R rating matrix):
- User factors matrix ($H$)
-
Movie factor matrix ($W$)
$D(R | W,H)=\frac{1}{2}||R - WH||^{2}_{F} + \\ {\alpha}_{l1w}||W|| + {\alpha}_{l2w}||W||^{2}_{F} + \lambda_{l1h}|H||| + \lambda_{l2h}||H||^{2}_{F}$
Regularized Alternating Least Square (RALS)
Fixed-point RALS Algorithm: Equating gradient to zero, obtain iterative update scheme of $W$, $H$
- estimate $H$, given $W$ (inner loop: tolerance based solutions are provided )
- enforce positivity (NMF)
- REPEAT until convergence (outer loop: factor matrices are updated until convergence)
Current effort aims to introduce flexibility to impose additional constraints (e.g. bounds on variables, sparsity, etc.)
NMF - Essentially Clustering
$D(R | W,H)=\frac{1}{2}\sum^{n}_{i=1}||r_{i}-Wh_{i}||^{2}_{2}$
Solve $n$ independent problems:
-
$min_{h_{i}\ge 0} \frac{1}{2} ||r_{i}-Wh_{i}||^{2}_{2}$
-
Aggregated solutions: $H=[h_{1},h_{2},h_{3},…h_{n}]$
Our contribution: given $W$, we compute cluster possibilities ($H$) using a QP solver in Spark Mllib. (Note: This is inner loop)
QP to ADMM/SOCP
-
ADMM : solves by decomposing a hard problem into simpler yet efficiently solvable sub-problems and let them achieve consensus.
QP to ADMM/SOCP
-
ADMM : solves by decomposing a hard problem into simpler yet efficiently solvable sub-problems and let them achieve consensus.
-
ECOS: solves a specific class of problems that can be formulated as a second-order cone program (SOCP) using primal-dual interior-point method.
QP to ADMM/SOCP
- Use: Our priliminary investigation shows that ADMM solves certain class of problems (e.g. bounds, l1 minimization) much faster than ECOS while the later proves effective in handling relatively complicated constraints (e.g. equality constraints).
QP: ADMM formulation
Objective $f(h): 0.5||r-Wh||^{2}_{2} => 0.5h^{T}(WW^{T})h - (r^{T}W)h$
Constraints $g(z) : z >= 0$
ADMM formulation $f(h) + g(z) \\ \text{s.t } h = z$
ADMM Steps
- $h^{k+1} = argmin_{h} f(h + 0.5 \times \rho ||h - z^{k} + u^{k}||_{2}^{2})$
- $z^{k+1} = h^{k+1} + u^{k} \text{s.t } z^{k+1} \in g(z)$
- $u^{k+1} = u^{k} + h_{k+1} - z_{k+1}$
QP: ADMM Implementation(I)
class DirectQpSolver(nGram: Int,
lb: Option[DoubleMatrix] = None, ub: Option[DoubleMatrix] = None,
Aeq: Option[DoubleMatrix] = None,
alpha: Double = 0.0, rho: Double = 0.0,
addEqualityToGram: Boolean = false) = {
def solve(H: DoubleMatrix, q: DoubleMatrix,
beq: Option[DoubleMatrix] = None): DoubleMatrix = {
wsH = H + rho*I
solve(q, beq)
}
def solve(q: DoubleMatrix, beq: Option[DoubleMatrix]): DoubleMatrix = {
//Dense cholesky factorization
val R = Decompose.cholesky(wsH)
ADMM(R)
}
QP : ADMM Implementation(II)
def ADMM(R: DoubleMatrix): DoubleMatrix = {
rho = 1.0
alpha = 1.0
while (k ≤ MAX_ITERS) {
scale = rho*(z - u) - q
// x = R \ (R' \ scale)
solveTriangular(R, scale)
//z-update with relaxation
zold = (1-alpha)*z
x_hat = alpha*x + zold
z = xHat + u
Proximal(z)
if(converged(x, z, u)) return x
k = k + 1
}
}
QP: SOCP formulation
Objective transformation $\text{minimize } t \\ \text{ s.t } 0.5h^{T}(WW^{T})h - (r^{T}W)h \leq t$
Constraints $h >= 0 \\ Aeq \times h = Beq \\ A \times h \leq B$
Quadratic constraint transformation
QP: SOCP Implementation
class QpSolver(nGram: Int, nLinear: Int = 0, diagonal: Boolean = false,
Equalities: Option[CSCMatrix[Double]] = None,
Inequalities: Option[CSCMatrix[Double]] = None,
lbFlag: Boolean = false, ubFlag: Boolean = false) = {
NativeECOS.loadLibraryAndCheckErrors()
def solve(H: DoubleMatrix, f: Array[Double]): (Int, Array[Double]) = {
updateHessian(H)
updateLinearObjective(f)
val status = NativeECOS.solveSocp(c, G, h, Aeq, beq, linear, cones, x)
(status, x.slice(0, n))
}
}
Use Case: Positivity
Application: Image feature extraction / energy spectrum where negative coefficients or factors are counter intuitive
| OCTAVE | ALS | ECOS | ADMM | ||
|---|---|---|---|---|---|
| Negative Coefficients: | 0 | 2 | 0 | 1 | |
| RMSE: | N.A. | 2.3e-2 | 3e-4 | 2.7e-4 |
Use Case: Positivity
//Spark Driver
val lb = DoubleMatrix.zeros(rank, 1)
val ub = DoubleMatrix.zeros(rank, 1).addi(1.0)
val directQpSolver = new DirectQpSolver(rank, Some(lb), Some(ub)).setProximal(ProjectBox)
val factors = Array.range(0, numUsers).map { index =>
// Compute the full XtX matrix from the lower-triangular part we got above
fillFullMatrix(userXtX(index), fullXtX)
val H = fullXtX.add(YtY.get.value)
val f = userXy(index).mul(-1)
val directQpResult = directQpSolver.solve(H, f)
directQpResult
}
Use Case: Positivity
//DirectQpSolver Projection Operator
def projectBox(z: Array[Double], l: Array[Double], u: Array[Double]) {
for(i <- 0 until z.length) z.update(i, max(l(i), min(x(i), u(i))))
}
Use Case: Sparsity
Application: signal recovery problems in which the original signal is known to have a sparse representation
| OCTAVE | ALS | ECOS | ADMM | ||
|---|---|---|---|---|---|
| Non-Sparse Coefficients: | 16 | 20 | 18 | 18 | |
| RMSE: | N.A. | 9e-2 | 2e-2 | 2e-2 |
Use Case: Sparsity
//Spark Driver
val directQpSolverL1 = new DirectQpSolver(rank).setProximal(ProximalL1)
directQpSolverL1.setLambda(lambdaL1)
val factors = Array.range(0, numUsers).map { index =>
// Compute the full XtX matrix from the lower-triangular part we got above
fillFullMatrix(userXtX(index), fullXtX)
val H = fullXtX.add(YtY.get.value)
val f = userXy(index).mul(-1)
val directQpL1Result = directQpSolverL1.solve(H, f)
directQpL1Result
}
Use Case: Sparsity
//DirectQpSolver Proximal Operator
def proximalL1(z: Array[Double], scale: Double) {
for(i <- 0 until z.length)
z.update(i, max(0, z(i) - scale) - max(0, -z(i) - scale))
}
Use Case: Equality with bound
Application: Support Vector Machines based models with sparse weight representation or portfolio optimization
| OCTAVE | ALS | ECOS | ADMM | ||
|---|---|---|---|---|---|
| Sum of Coefficients: | 1 | - | 0.99 | 1 | |
| Non-Sparse Coefficients: | 4 | - | 4 | 4 | |
| RMSE: | N.A. | 1.1 | 2e-4 | 5.5e-5 |
Use Case: Equality with bounds
//Equality constraint x1 + x2 + ... + xr = 1
//Bound constraint is 0 ≤ x ≤ 1
val equalityBuilder = new CSCMatrix.Builder[Double](1, rank)
for (i <- until rank) equalityBuilder.add(0, i, 1)
val qpSolverEquality =
new QpSolver(rank, 0, false,
Some(equalityBuilder.result), None, true, true)
qpSolverEquality.updateUb(Array.fill[Double](rank)(1.0))
qpSolverEquality.updateEquality(Array[Double](1.0))
Use Case: Equality with bounds
val factors = Array.range(0, numUsers).map { index =>
fillFullMatrix(userXtX(index), fullXtX)
val H = fullXtX.add(YtY.get.value)
val f = userXy(index).mul(-1)
val qpEqualityResult = qpSolverEquality.solve(H, f)
qpEqualityResult
}
Runtime Experiments (in ms)
Dataset: Movielens 1M ratings from 6040 users on 3706 moviesExample run
MASTER=local[1] run-example mllib.MovieLensALS --rank 25 --numIterations 1 --kryo --qpProblem 1 ratings.dat
Algorithms variants
Quadratic Minimization(QP), with Positivity(QpPos), bounds(QpBounds), Sparsity(QpL1), Equality and Bounds(QpEquality)
| LS | ECOS | ADMM | ||
|---|---|---|---|---|
| Qp | (30)+(57) | (3826)+(6943) | (99)+(143) | |
| QpPos | (98)+(320) | (6288)+(11975) | (265) + (2135) | |
| QpBounds | (39)+(55) | (6709)+(11951) | (1556)+(1329) | |
| QpL1 | (54)+(80) | (32171)+(58766) | (352)+(1593) | |
| QpEquality | (63)+(133) | (5231)+(7912) | (14681)+(65893) |
QP : Default ADMM
def ADMM(R: DoubleMatrix): DoubleMatrix = {
rho = 1.0
alpha = 1.0
while (k ≤ MAX_ITERS) {
scale = rho*(z - u) - q
// x = R \ (R' \ scale)
solveTriangular(R, scale)
//z-update with relaxation
zold = (1-alpha)*z
x_hat = alpha*x + zold
z = xHat + u
Proximal(z)
if(converged(x, z, u)) return x
k = k + 1
}
}
Proximal Algorithms
QP: Accelerated ADMM
def ADMM(R: DoubleMatrix): DoubleMatrix = {
rho = 1.0
alpha = 1.0
while (k ≤ MAX_ITERS) {
zold = z
uold = u
alphaOld = alpha
scale = rho*(z - u) - q
// x = R \ (R' \ scale)
solveTriangular(R, scale)
//z-update without relaxation
z = x + u
Proximal(z)
updateRho(x,z,u)
if(converged(x, z, u)) return x
k = k + 1
//Nesterov's acceleration
alphaSolve = (1 + sqrt(1 + 4*alphaOld*alphaOld))/2
val alphaScaled = (1 - alphaOld)/alphaSolve
//z-acceleration
z = z + (z - zold)*alphaScaled
//u-acceleration
u = u + (u - uold)*alphaScaled
}
}
QP: Accelerated ADMM Matlab validation
Comparison of ECOS, MOSEK, ADMM and Accelerated ADMM for Matlab random matrices
Usecases
- QpSolver-Spark for unguided profile generation
- QpSolver-Spark for topic modeling
- Constrained Convex Minimizer: PLSA/LDA
Future work
- Release QpSolver-Spark after rigorous testing
- Runtime optimizations for QpSolver-Spark integration
- Release ECOS based LP and SOCP solvers based on community feedback
- Iterative Quadratic Minimizer with ADMM
- Constrained Convex Minimizer with ADMM
Questions
Join us and make machines smarter
References
- ECOS by Domahidi et al. https://github.com/ifa-ethz/ecos
- ADMM by Boyd et al. http://web.stanford.edu/~boyd/papers/admm/
- Proximal Algorithms by Neal Parikh and Professor Boyd